Δεν ξέρω αν το πήρατε χαμπάρι, αλλά δεν μάς μένει και πολύ χρόνος για σουλατσάρισμα στη γη. Δεν είναι οι Μάγιας, αυτούς προς το παρόν τους προσπεράσαμε, αλλά κάτι άλλο. Κάποια στιγμή, όχι πολύ μακριά από σήμερα, ο πληθυσμός της γης θα χτυπήσει άπειρο! Κυριολεκτικά! Θα γίνουμε τόσοι, που δεν θα 'χουμε τόπο να σταθούμε, θα ξεχειλίζουμε από τις άκρες της και θα πηδάμε στο κενό από το στρίμωγμα. Δεν θα γίνουμε απλώς πολλοί, ούτε υπερβολικά πολλοί, αλλά άπειροι!
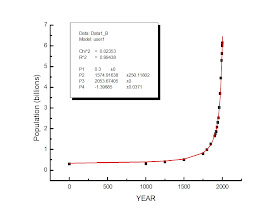
Το παραπάνω διαγραμματάκι δείχνει στον οριζόντιο x-άξονα τα χρόνια από το 0 μΧ μέχρι το 2001, και στον κάθετο, τον πληθυσμό της Γης για όσες χρονιές είναι διαθέσιμα στοιχεία, σε δισεκατομμύρια. Κάθε τετραγωνάκι αντιστοιχεί στον πληθυσμό μιας δεδομένης χρονιάς οι οποίοι έχουν ληφθεί από διάφορες αξιόπιστες data-bases.
Η κόκκινη γραμμή είναι το fit, δηλαδή η αναλυτική συνάρτηση που περνάει όσο το δυνατόν εγγύτερα από τα δεδομένα. Η αναλυτική έκφραση είναι ο γνωστός μας από άλλες αναρτήσεις (βλ. Θαυμαστός κόσμος των Αμμολόφων) Power Law και στη συγκεκριμένη περίπτωση δίνεται από την εξής έκφραση:
όπου η μεταβλητή P είναι ο πληθυσμός, X είναι τα χρόνια και Xc είναι η κρίσιμη χρονιά για την οποία ο πληθυσμός θα πάει στο άπειρο. Α και a είναι η πολλαπλασιαστική σταθερά και ο εκθέτης αντίστοιχα.
Όπως φαίνεται από το διάγραμμα, η κόκκινη γραμμή η οποία αναπαριστά πολύ καλά τα δεδομένα,έχει ληφθεί για το έτος Xc=2054, το οποίο δεν είναι και πολύ μακριά!
Για να μην τρομάξουμε όμως υπερβολικά, εξίσου καλό fit λαμβάνεται και για τη χρονιά 2080, αλλά όχι για αργότερα. Δηλαδή, αν καβατζάρουμε το 2050, σίγουρα θα κολλήσουμε στο 2080.
Ποια είναι η λύση λοιπόν; Μα φυσικά ο πόλεμος! Πόλεμος όμως κανονικός, όχι τα παιχνιδάκια του Α και του Β παγκοσμίου πολέμου. Θα πρέπει να γίνουν σοβαρά πληθυσμιακά κουρέματα, του στιλ PSI+ και PSI++ και ακόμα παραπάνω.
Νομίζω ότι η παρούσα κρίση είναι ένα σημαντικό προεόρτιο. Ο πλανήτης θα ξεφορτωθεί κάποιο παραπανίσιο φορτίο ανθρώπων, αλλά χρειάζεται μια διαδοχή από σοβαρότερες κρίσεις, ώστε να αναστραφεί η τάση της πληθυσμιακής αύξησης. Πολλές κρίσεις στη σειρά, μοιραία θα φέρουν και τον Πόλεμο, που τόσο χρειαζόμαστε, ώστε όσοι επιβιώσουν να μπορούν να ζήσουν με κάποια άπλα.
Κοιτάω τις ημερομηνίες λήξεις των ομολόγων. Γαμώτο! Τα περισσότερα λήγουν πριν το 2030. Τουλάχιστον θα γλιτώναμε μερικά και δεν θα τα πληρώναμε, αφού θα καταστρεφόταν ο κόσμος. Ευτυχώς, οι μικρο-ομολογιούχοι θα προφτάσουν να εισπράξουν τα ομόλογα που τους έχουν απομείνει. Κάτι είναι και αυτό...
Υ.Γ. Τα data είναι από United Nations Population Division, Dept. of Economic and Social Information and Policy Analysis.
Αν πάρουμε τους λογάριθμους και στα δυο μέλη της εξίσωσης, έχουμε
log(P-P0)=logA-alog(Xc-X)
η οποία παριστάνει μια ευθεία γραμμή. Xc=2054. Η κόκκινη καμπύλη είναι ευθεία και περνάει τζάμι από τα σημεία, δηλαδή τους πληθυσμούς. Οι χρονιές στο διάγραμμα αυτό ανεβαίνουν από τα δεξιά προς τ' αριστερά.
Μια χαρά, λοιπόν θα βγάλουμε κοριούς το 2054!


Μπα... εγώ φοβάμαι το 4.500.2012 μΧ, τότε θα γίνει ο Ήλιος "κόκκινος γίγαντας" και θα ψηθούμε όλοι.
ΑπάντησηΔιαγραφήΑν και το 2054 είναι 1000 χρόνια μετά το σχίσμα...
Ειδες που ταιριάζει με το σχισμα? Αυτο ειναι πολύ δυνατο σημαδι!
ΑπάντησηΔιαγραφήΝα μην εχεις καμια αμφιβολία. Δεν θα χρειαστει να περιμενουμε τοσο μακρια, ωσπου ο ηλιος να γινει κοκκινος γιγαντας.
Το τέλος ειναι πολυ κοντά...
διάγραμμα ράντας ...
ΑπάντησηΔιαγραφήΤι ειναι το "ραντας"
ΑπάντησηΔιαγραφήΠολλές φορές το έχω δει αυτό το διάγραμμα (ή σχετικά). Το πρόβλημα ειναι ότι περιγράφουν το "θα" και όχι το "αν".
ΑπάντησηΔιαγραφήΔηλαδή: με βάση το παρελθόν λένε πως ΘΑ γίνει αυτό. Στην πραγματικότητα, όμως, αυτό ΘΑ γίνει ΑΝ συνεχίσει έτσι η πορεία, κάτι για το οποίο αμφιβάλλω... όχι πως δεν υπάρχει χοντρό πρόβλημα, αλλά το όλο θέμα είναι απείρως πιο πολύπλοκο από μία στατιστική ανάλυση στο γόνα.
ειναι εντυπωσιακο, ομως οτι η πληθυσμιακη αυξηση ακολουθει αυτο το pattern για 1000 χρονια, οπου στη διαρκεια αυτων εχουμε μεταβολη και του ρυθμου αυξησης.
ΑπάντησηΔιαγραφήΗ αναλυτικη συναρτηση που εδωσα περιγραφει με αξιοσημειωτη ακριβεια τα δεδομενα, και δεν φαινεται να επηρεάζεται από εκείνες τις περιόδους όπου ειχαμε σημαντικές μειώσεις πληθυσμών. Αυτες δεν αποτυπώνονται σαν παρεκκλίσεις.
Φυσικά όλα τα extrapolation στο χρονο πρεπει να τα βλεπουμε με μια δοση σκεπτικισμού, αλλά και πάλι, 1000 χρονια να πεφτουν πάνω σε μια απλή εξισωση, δεν είναι μικρό πράγμα.
Εν γενει τα population dynamics έχουν τη δομη fractal. To Logistic map (για τον πληθυσμό των κουνελιών) και το Power Law (εδω)κρύβουν φρακταλικές δομές.
Δεν αμφισβητώ την ορθότητα και το fit της συνάρτησης. Αυτό που λέω είναι ότι είναι πολύ απλοϊκή για την πρόβλεψη σε σημεία τα οποια είναι καταφανώς ασταθή.
ΑπάντησηΔιαγραφήΕίμαι σίγουρος ότι η συνάρτηση που περιγράφει τη θερμοκρασία του νερού στο μπρίκι μου είναι πολύ ακριβής, όσο πλησιάζει όμως τους 100 βαθμούς πάει κατά διαόλου και παύει να ισχύει εντελώς.
Έτσι κι εδώ. Είναι πολύ ενδιαφέρον το ότι οι θεωρίες και η συνάρτηση περιλαμβάνουν πολύ περισσότερα δεδομένα από ένα απλό prospensity to procreate ακόμη και στα κουνελάκια - ήτοι, πολλούς εξωτερικούς παράγοντες. Έτσι κι εδώ, θεωρώ ότι η τάση θα αναστραφεί εξωγενώς - όχι απαραίτητα από έλλειψη τροφής, αλλά, π.χ., από εκπαίδευση. Ή βελτίωση συνθηκών υγιεινής (όπως είπε και ο Gates και το έχουν κάνει σημαία οι αντι-εμβολιαστές).
Συμφωνω, μπορεί να μην μπορείς να περιγράψεις τι συμβαινει γυρω απο μια singularity, αλλά τη singularity την ξερεις ακριβως. Για παράδειγμα η θερμοκρασια βρασμου ειναι γνωστή και ειναι 100οC ακριβως.
ΑπάντησηΔιαγραφήΝαι αλλά εδώ επιλέγεις μία δραματική, η οποία ουδόλως είναι βέβαιο ότι θα επιτευχθεί... αυτό λέω, πως υπάρχει μεγάλη πιθανότητα να αναστραφεί η πορεία πολύ πριν από το σημείο αυτό.
ΑπάντησηΔιαγραφήΤέλος πάντων, δεν έχει μεγάλη σημασία, νομίζω πως είναι προφανές. Διαφωνώ for the fun of it :D
τα ξαναλεμε σε καμια 20αρια χρονια. Το που παει το πραγμα, θα εχει αρχισει να φαινεται..
ΑπάντησηΔιαγραφήΚάτσε, μιλάς από το '12 ή το '13 τώρα; :)
ΑπάντησηΔιαγραφήΣτα οικονομικά ράντα είναι η επανακεφαλαιοποίηση των τόκων και η σταδιακή αύξηση του κεφαλαίου.
ΑπάντησηΔιαγραφήΣιγά σιγά με το ίδιο επιτόκιο το κεφάλαιο αρχίζει και αυξάνει με πρόοδο.
Από κάποιο σημείο καμπής και μετά η απόδοση, δηλαδή κεφάλαιο + τόκοι αποκτούν τρελή άνοδο, κάπου 15 χρόνια μετά. Τότε η καμπύλη αρχίζει και ανεβαίνει κάθετα...
Κοπρια,
ΑπάντησηΔιαγραφήΔεν ειναι το ιδιο πραγμα με το κεφάλαιο, εφ' όσον το επιτοκιο παραμενει σταθερο στο χρονο.
Κν=Κο*(1+α)^ν, όπου ν είναι το χρονικό διάστημα.
Για να εχεις το ιδιο αποτελεσμα με την πληθυσμιακή αυξηση θα πρεπει το επιτοκιο να αυξάνει με το χρόνο. Στην πραγματικότητα, αυτό συμβαινει με τον πληθυσμο: το rate εξαρταται από τον χρόνο.
Παιδιά, ηρεμείστε!
ΑπάντησηΔιαγραφήΜε τους σημερινούς ρυθμούς αύξησης του παγκόσμιου πληθυσμού θα έχουμε φτάσει σε περίπου 20 δισεκατομμύρια μετά από 80 χρόνια.
Με δεδομένο ότι σήμερα μόνο το 10% της ξηράς καλλιεργείται και ότι τα περιθώρια αύξησης της επιφάνειας αυτής είναι τεράστια, καθώς και οι καλλιεργητικές μέθοδοι, υπολογίζεται (πάντα με εναλλακτικές πλην δόκιμες επιστημονικά, μεθόδους υπολογισμού, που αμφισβητούν τις κρατούσες επίσημες), ότι η μάνα γη μας μπορεί να θρέψει άνετα πλέον των 40 δις ανθρώπων.
Ορθρολογική διαχείρηση χρειάζεται και ένας παγκόσμιος χωροταξικός σχεδιασμός που θα βάλει τάξη στη "χαοτική" καπιταλιστική επέκταση....
Γενικά ισχύει το "Όλοι οι καλοί χωράνε"
Χρόνια Καλά!
Πάντως, το μοντελάκι βγαζει ότι ο κοσμος θα έχει γινει ...άπειρος, μέχρι το 2054, άντε βία μέχρι το 2080. Δεν θετει καν θεμα διατροφής. Απλώς χώρου!
ΑπάντησηΔιαγραφήΤο ότι μετά 80 χρονια, θα ειμαστε 20 δις, από ποιο μοντέλο βγαίνει;
Χρόνια πολλά και καλά!
Στατιστικά στοιχεία ΟΗΕ για τον παγκόσμιο πληθυσμό 2010 και ρυθμός αύξησής του περίπου 1,3% ετησίως, από τις ίδιες αξιόπιστες πηγές.
ΑπάντησηΔιαγραφήΌσον αφορά στον "χώρο", πάλι με δεδομένο ορθολογικό σχεδιασμό αρκεί μόλις το 5% της ξηράς για να φιλοξενήσει με απόλυτα άνετες συνθήκες όλον αυτό τον πληθυσμό (40 δις). Σήμερα η έκταση που καταλαμβάνουν οι αστικές και ημιαστικές περιοχές του πλανήτη μόλις καταλαμβάνουν το 1,5% της ξηράς και μάλιστα με ένα εντελώς ανορθολογικό τρόπο.
Μην ακούτε τους καπιταλιστές που τρέμουν στην ιδέα, ότι η αύξηση των μαζών θα οδηγήσει σε συνθήκες ανατροπής της κυριαρχίας τους!
Ναι μπορεί να οδηγηθούμε και σε Πόλεμο ακόμα προκειμένου να ανακοπεί η αύξηση του πληθυσμού, ή να μειωθεί κιόλας, όχι όμως γιατί αντικειμενικά δεν χωράμε, αλλά γιατί για την επιβίωση της ανθρωπότητας απαιτείται ανατροπή του σημερινού status......
τα στατιστικα μπορει να ειναι απο την ιδια πηγη, (ΟΗΕ), αλλά το μοντελο που χρησιμοποιω είναι διαφορετικο.
ΑπάντησηΔιαγραφήΗ διαφορα μας ειναι οτι υποθετεις σταθερο ρυθμο αυξησης ισο με 0.013, ενω το μοντελο που προτεινω υποθετει οτι ο ρυθμος αυξησης μεταβαλλεται με το χρονο.
Για να δουμε τι δινει το μοντελο του σταθερου ρυθμου αυξησης, ισου με 0.013:
Αν παρουμε το διαστημα από 1900 εως 2001, τοτε ναι μεν τα ακρα τα πιανει, στα ενδιαμεσα ομως ξεφευγει κατά πολύ.
Παραδειγμα:
για το 1950, ο πραγμ. πληθ ειναι 2,52 δις, ενώ το μοντελο δινει 3,19 δις. Για το 1980, πραγμ=4,45 δις, ενω το μοντελο=4,70 δις, κ.ο.κ.
Αν πάρεις και εφαρμοσεις τον ιδιο κανονα στο διαστημα 1000-2001, τοτε εκει αποτυγχάνει εντελώς.
Μπορεις να το δοκιμασεις σε ενα calculator εφαρμοζοντας τον ιδιο τυπο για το κεφαλαιο και τον τοκο που εδωσα πριν.
Το θεμα με τον πληθυσμο το επιασα περισσότερο σαν ενα μαθηματικο παιχνιδι, και ομολογω ότι με εντυπωσιασε. Δεν περιμενα μια τοσο απλη εξισωση να αναπαριστα με τοση ακριβεια πληθυσμους από το 1000 μεχρι το 2000.
Καλη χρονια!
ψάχνω ακόμα το μαύρο κύκνο!!!
ΑπάντησηΔιαγραφήκαλή χρονιά!
Κοίτα, πότε θα καταστραφούμε δεν το ξέρω, το ότι τον πόλεμο όμως τον έχουμε σίγουρο έτσι όπως πάμε, στο υπογράφω!
ΑπάντησηΔιαγραφήΗ αποτυχία των υπολογιστικών μοντέλων, έχουν να κάνουν με την ευθεία προβολή σημερινών δεδομένων στο μέλλον.
ΑπάντησηΔιαγραφήΑπό πουθενά δεν προκύπτει ότι ο ρυθμός αύξησης του πληθυσμού θα παραμένει κατά μέσο όρο σταθερός, όπως ισχυρίστηκα εγώ, αλλά επίσης, ότι θα είναι μεταβαλλόμενος και μάλιστα αυξητικός, όπως αντίστοιχα ισχυρίζεσαι εσύ.
Ποικιλία παραγόντων μπορεί να επηρεάσει αυτόν το ρυθμό και πολύ φοβούμαι ότι μετά από τα 42 χρόνια της δικής σου πρόβλεψης, προσωπικά δεν θα με αφορά καθόλου το ζήτημα.
Εκείνο που ήθελα να καταδείξω παρεμβαίνοντας στη συζήτηση, είναι ότι πολύ λιγότερο πρέπει να μας ανησυχεί ο υπερπληθυσμός και πολύ περισσότερο οι πολιτικές για τον έλεγχό του, που ήδη εφαρμόζονται από τις εξουσιαστικές ελίτ και θα τις δούμε να ξεδιπλώνονται με ένα απίθανα κτηνώδη τρόπο, στα όρια πραγματικής γενοκτονίας, τα προσεχή χρόνια, ακριβώς για να μη θιγεί στο απειροελάχιστο η δική τους επικυριαρχία.
Εμείς πρέπει να δείξουμε ότι μπορούμε να ζήσουμε καλύτερα κι ας γίνουμε περισσότεροι. Η γη μας απέχει πολύ από το να κορεστεί από τη παρουσία μας, αρκεί και εμείς να τη σεβόμαστε.
Κι από 'μένα Καλή Χρονιά σε όλες κι όλους!
Χρονια πολλά Geokalp!,
ΑπάντησηΔιαγραφήΔεν τον βλέπουμε, γιατί μάς έχει κάτσει από πάνω, εδω και τρια τεσσαρα χρονακια!
Darthiir,
ΑπάντησηΔιαγραφήεχεις κανενα μοντελο για τους πολεμους? :))
Καλη χρονια!
τωρα θυμηθηκα, που ειχα γραψει ενα ποστ πριν 2,5 χρονια για
ΑπάντησηΔιαγραφήΤον Μύθο του Υπερπληθυσμού
και πώς χρησιμοποιείται. Σιγουρα η εξουσια μπορει καλλιστα να εκμεταλλευτει το θεμα ιδεολογικα και να επιβαλει πολιτικες ελεγχου του πληθυσμού. Γιαυτο και παιζει παντα στο background,αν και ακομα υποτονικά.
Είμαι στη διαδικασία ανάπτυξης!
ΑπάντησηΔιαγραφήΚαλή Χρονιά και σε σένα!
Χαίρε, Cynical - και χρὀνια μας πολλά:) Καλά τα γράφεις, mathematically speaking, αλλά (για να παραφράσω το σχόλιο του Gryzor) η ανάλυση μάς λέει τί (πιθανά) θα συμβεί εάν συνεχίσουμε τον ίδιο δρόμο. Και αυτό με βάση την προσαρμογή των δεδομένων του παρελθόντος ως προς στην κύρια (εκθετική) συνιστώσα - και όχι σε στοιχεία του μρφοκλασματικού (fractal) χαρακτήρα (εκεί, στα περίεργα, είναι τα δύσκολα :)
ΑπάντησηΔιαγραφήΓεια σου Prths, και Καλη Χρονια!
ΑπάντησηΔιαγραφήΣτην singularity πρακτικα δεν φτανεις ποτε, γιατι η φυση απεχθανεται τους απειρισμους. Τωρα, οσο φτανεις σε ενα κρισιμο σημειο, οπως ο εν λόγω χρονος, εκεί εχεις διακυμανσεις της πυκνοτητας σε ολες τις κλιμακες. Δηλ, μπορει να συμβαινει το ιδιο και με τον πληθυσμο.
Παραπάνω δεν ξερω. Επειδη το θεμα εχει ενδιαφερον, υποσχομαι να το ψαξω περισσότερο. Παντως, πολλοί εχουν καταπιαστε με δαυτο.
Αγαπητή κυνική, διαβάζω εδώ και καιρό το blog σου και δηλώνω ενθουσιασμένη! Ο λόγος που σου γράφω είναι κυρίως για να σου προτείνω ένα άρθρο αλλα επίσης και μια στήλη που μπορεί να σου αρέσει. Το άρθρο μπορείς να το βρείς αν κλικάρεις πάνω στο όνομά μου. Η στήλη είναι η sci-zophrenia και έχει πολλά ενδιαφέροντα άρθρα. Ο αρθρογράφος της στήλης μου θυμίζει αρκετά το δικό σου σκεπτικό!
ΑπάντησηΔιαγραφήΣ' ευχαριστω end of the world
ΑπάντησηΔιαγραφήpoly kalo to link! θα το εξερευνησω..